Условие задачи:
Чему равен максимальный угол наклона плоскости к горизонту, если на этой плоскости удерживается груз? Коэффициент трения между грузом и плоскостью равен 0,413. Ответ дать в градусах.
Дано:
\(\mu = 0.413\)
Найти:
\(\alpha_{max}\)
Решение:
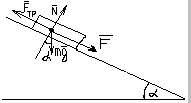Так как груз по плоскости не движется, то его ускорения равняется нулю. А значит, по второму закону Ньютона, проекция силы тяжести на линию движения, запишется так:
\(F = m*g*sin(\alpha)\)
Эта проекция меньше силы трения:
\(F_{tr} = \mu*N=\mu*m*g*cos(\alpha)\)
А значит, можем получить отношение, а затем выразить из него искомую величину - максимальный угол удержания груза:
\(sin(\alpha_{max}) = \mu*cos(\alpha_{max})\)
\(\alpha_{max} = atan(\mu)\)
Подставим числовое значение и получим ответ:
\(\alpha_{max} = 22.44 ^{\circ}\)
Решение картинкой:
