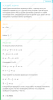
Через укрепленный блок перекинута нить, к одному концу ее подвешен первый груз, а к другому концу второй и третий грузы последовательно. Массы грузов одинаковы и равны 8 кг. Найти натяжение нити, связывающей второй и третий грузы. Блок считать невесомым. Трением в блоке пренебречь.
\(m=8 кг.\)
Найти: \(Т_{1}-?\)
По второму закону Ньютона:
\(2\cdot m\cdot g-T=2\cdot m\cdot a \); (1)
\(T-m\cdot g=m\cdot a\); (2)
\(m\cdot g-T_{1}=m\cdot a\); (3)
Складывая (1) и (2):
\(2\cdot m\cdot g-m\cdot g=3\cdot m\cdot a;\)
\(m\cdot a=\frac{1}{3}\cdot m\cdot g;\)
Подставляем последнюю формулу в (3) получаем:
\(m\cdot g-T_{1}=\frac{1}{3}\cdot m\cdot g;\)
\(T_{1}=\frac{2}{3}\cdot m\cdot g;\)
В полученную формулу осталось подставить числовые значения из условия задачи. Так же необходимо помнить что ускорение свободного падения g = 9.8 м/с.
\(T_{1}=52.302 H.\)