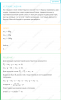
На гладком столе лежит брусок массой 9 кг. К бруску привязаны два шнура, перекинутые через невесомые блоки, прикрепленные к противоположным краям стола. К концам шнуров подвешены гири, массы которых 1 кг и 10 кг. Найти ускорение, с которым движется брусок. Массой блоков и трением пренебречь.
\(m_{1}=9kg\)
\(m_{2}=1kg\)
\(m_{3}=10kg\)
Найти:
\(a\)
Для висящих грузов второй закон Ньютона запишется:
\(T_{2}-m_{2}\cdot g=m_{2}\cdot a\) (2)
\(m_{3}\cdot g-T_{3}=m_{3}\cdot a\) (3).
Для груза на столе: \(T_{3}-T_{2}=m_{1}\cdot a\).
Выражая \(T_{2}\) и \(T_{3}\) из (2) и (3) и подставляя их в это уравнение получаем:
\(m_{3}\cdot g-m_{3}\cdot a-m_{2}\cdot a-m_{2}\cdot g=m_{1}\cdot a\),
откуда \(a=\frac{m_{3}-m_{2}}{m_{1}+m_{2}+m_{3}}\cdot g\).
Подставим значения из дано и получим
Ответ: \(a=4.413 s^{-2}\cdot m\)