Решение задачи: Найти гравитационное давление внутри земного шара в модели однородной

Представим, что земля - шар массой M и радиусом R. Выделим внешний слой на шаре, который давит на ядро.

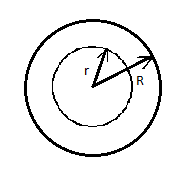
Ускорение свободного падения на расстоянии r от ядра:

\(g (r) = \gamma {M \over R^2 }\cdot {r \over R}\), 

где \(\gamma\) - гравитационная постоянная.

Давление внешнего слоя на шар:

\(p(r) = \int_{R}^{r} \rho g(r) dr\), подставим g(r) :

\(p(r) = \int_{R}^{r} \rho \gamma {M\cdot r \over R^3 } dr\) \(= \rho \gamma {M \over R^3 } \cdot ({R^2 - r^2 \over 2});\)

\(p(r) = \gamma {M \over 2R} \rho (1-{r^2 \over R^2})\) (1) ,

где \(\rho\) - плотность несжимаемой земли.

\(\rho = {M \over V} = {M \over 4/3 \pi R^3} \) (2).

Подставив (2) в (1) получим: 

\(p(r) = {3 \over 8 \pi}{\gamma M^2 \over R^4} (1- {r^2 \over R^2})\) - Зависимость давления в зависимости от расстояния до центра в модели несжимаемой жидкости.

В центре r = 0

\(p = {3 \over 8 \pi}{\gamma M^2 \over R^4} \)

Из справочников берем:

R = 6371 км = 6371000 м

M = 5,9726 * 10²⁴  кг

\(\gamma\) = 6,67 * 10^-11 \({м^3 \over с^{-2} кг }\)

Подставляя получаем:

\(p = {3 \over 8 \cdot 3,14}{6,67 \cdot 10^{-11} \cdot 5,97^2 \cdot 10^26 \over 6371^4 \cdot 10^7} \) \(= 1,752 \cdot 10^{11} [{кг \over с^2 \cdot м^2}]\)\( = 1,752 \cdot 10^{11} Па\)

Ответ: гравитационное давление внутри земного шара в модели однородной несжимаемой жидкости. будет равно 1,752 * 10¹¹ Па