Условие задачи:
По наклонной плоскости, составляющей с горизонтом угол 27 град., скользит тело. Пройдя расстояние 192 м, тело приобретает скорость 19 м/с. Чему равен коэффициент трения тела о плоскость.
Дано:
\(\alpha =27 град\)
\(S=192м\)
\(V=19\frac{м}{с}\)
Найти:
\(\mu\)
Решение:
По второму закону Ньютона
\(F-F_{тр}=F-\mu\cdot N=m\cdot a.\)
Из проекции на ось X \(F=m\cdot g\cdot sin(\alpha ),\)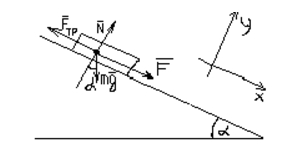
на ось y - \(N=m\cdot g\cdot cos(\alpha ).\)
Тогда \(m\cdot g\cdot [sin(\alpha )-\mu\cdot cos(\alpha )]=m\cdot a_{1},\)
где ускорение найдется из формулы \(a=\frac{V^{2}}{2\cdot S}.\)
Итак, \(\mu=tan(\alpha)-\frac{V^{2}}{2\cdot g\cdot S\cdot cos(\alpha)}.\)
Ответ: \(\mu=0.402\)
Решение картинкой:
