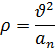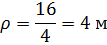По заданным уравнениям движения требуется найти: уравнение траектории, скорости по осям X и Y, ускорение по осям X и Y, касательное и нормальное ускорения, а также радиус кривизны в момент времени \(t_0 = \pi/3\).
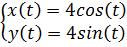
Уравнение траектории представляет собой зависимость координаты Y от X, исключая время для этого выразим cos(t) и sin(t) из обоих уравнений и возведем в квадрат:
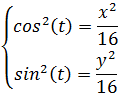
Складываем оба уравнения:
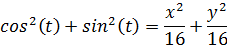
Слева известное тригонометрическое выражение:
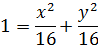
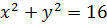
В результате получили уравнение окружности с радиусом R=4;
Скорость есть первая производная по времени от соответствующей координаты:
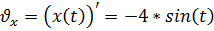
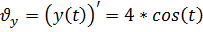
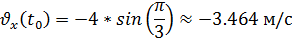
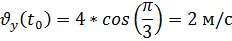
Модуль скорости точки:
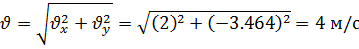
Ускорение – есть первая производная от скорости:
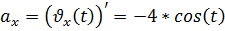
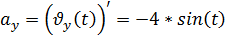
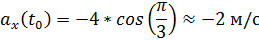
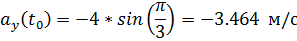
Модуль полного ускорения:
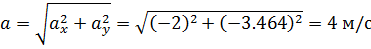
Модуль касательного ускорения точки:
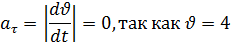
Модуль нормального ускорения точки:
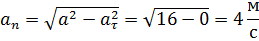
Радиус кривизны: