Условие задачи:
Небольшой груз подвешен на нити к подставке, укрепленной на тележке. Тележка движется по горизонтальной плоскости с ускорением равным 4 м/с2. Масса груза равна 8 кг. Найти натяжение нити.
Дано:
\(a=4m\cdot s^{-2}\)
\(m=8kg\)
Найти:
\(T\)
Решение:
В системе отсчета мвязанной с тележкой на груз действует сила инерции равная \(F_{u}=-m\cdot a.\)
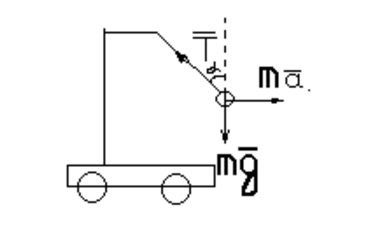Т.к. груз относительно тележки не движется, то сумма всех сил равна нулю.
Поэтому \(T\) равна результирующей сил \(-m\cdot \vec{a}\) и \(m\cdot \vec{g}\).
\(T:=\sqrt{(m\cdot a)^{2}+(m\cdot g)^{2}}\).
Ответ: \(T=84.728\) N
Решение картинкой:
